本文是面向交易实战的小波变换科普,代码为教学简化版(省略了标准小波的多层分解、阈值去噪、逆变换重构等复杂步骤),只保留核心思想:用小波系数对价格做多尺度平滑,提取趋势信息。适合策略开发和快速验证,不适合学术研究或论文发表。
经常刷知乎金融量化话题的朋友,肯定见过这样的场景:
某些"大神"张口闭口:
说得one愣one愣的,仿佛掌握了量化交易的***。
但你让他展示一下代码?
"这个...商业机密,不方便透露"
你让他解释一下原理?
"这个...涉及高等数学,说了你也不懂"
今天,我们就来探讨这些"知乎大神"经常挂在嘴边的内容,介绍小波变换在金融市场中的实际应用,帮助大家建立对这项技术的正确认识。
想象你在听一首歌,但录音里有杂音:
原始录音 = 人声 + 背景噪音 + 电流声
小波变换就像一个智能滤镜:
换到金融市场:
原始价格 = 真实趋势 + 短期波动 + 随机噪音
小波变换帮你:
小波变换的本质是用一组特定的"基函数"(小波)去分解原始信号。
想象你要描述一个人的长相:
在金融价格中:
原始价格序列 = 基函数1 × 权重1 + 基函数2 × 权重2 + ... + 噪音
基函数就是小波系数对应的"模板",不同的小波类型(Haar、Daubechies、Mexican Hat等)使用不同的模板,就像用不同的"特征提取器"去分解价格。
小波变换本质上是一个多尺度滤波器组:
高频滤波器 → 捕捉快速波动(日内噪音、tick级跳动)
中频滤波器 → 捕捉中期趋势(几小时到几天的波段)
低频滤波器 → 捕捉长期趋势(周级、月级的大方向)
为什么叫"小波"(wavelet)?
用正弦波分析金融价格的问题:正弦波假设信号是周期性重复的,但金融市场不是!BTC今天涨10%明天跌8%,完全不循环。
小波的优势:局部化分析。它能告诉你"在2025年12月20日下午3点到5点这段时间,价格主要是上涨趋势",而不是"整体市场在震荡"这种笼统的结论。
小波变换是可逆的,这很重要!
原始价格 ---> 小波分解---> 趋势成分 + 波动成分 + 噪音成分
趋势成分 + 波动成分 + 噪音成分 ---> 小波重构 ---> 原始价格
重构过程就是把分解后的各个成分有选择地组合回去:
分解后得到
重构时只用趋势成分
在实际交易中,我们通常只重构低频部分(趋势),把高频部分(噪音)直接丢掉。这就是小波"降噪"的原理。
不扯高深的积分公式,用大白话说:
小波变换 = 用一组“小波系数”对价格序列进行加权平均
基本公式:
平滑价格[i] = Σ(原始价格[i-j] × 小波系数[j]) / Σ(小波系数[j])
滤波器的视角:
原始价格通过小波滤波器 → 不同频率的成分被“筛选”出来
关键在于小波系数的选择:
举个例子:
假设你用Daubechies 4小波,系数是[0.483, 0.837, 0.224, -0.129]:
这组系数定义了一个滤波器:
当你把这个滤波器“滑动”扫过整个价格序列时,就完成了小波变换。每次滑动都在计算当前窗口内价格的加权平均,权重就是小波系数。
为什么能"分解"信号?
因为数学上可以证明:任何信号都可以表示为小波基函数的线性组合。就像任何颜色都可以用RGB三原色混合出来一样,任何价格序列都可以用小波基函数组合出来。不同的小波类型提供不同的”基函数库“,适合不同类型的信号分析。
在信号处理教科书中,小波变换通常包含复杂的多层分解、重构、阈值去噪等步骤:
完整的小波分析流程:
但在金融交易的实际应用中,我们不需要这么复杂。因为:
1. 交易只需要趋势方向,不需要完美重构
学术研究可能要求重构误差小于0.01%,但交易中只要能判断"涨还是跌"就够了。即使重构有5%的误差,只要趋势方向正确,策略就能盈利。
2. 实时性要求简化计算
完整的小波分解需要递归计算多层系数,在高频交易中会造成延迟。而直接卷积的方法可以在毫秒级完成,满足实盘需求。
3. 金融信号的特殊性
金融价格不是平稳信号,不存在严格的周期性。复杂的频率分解在这里意义不大,反而简单的趋势提取更实用。
因此,本文提取小波变换的精髓,专注于在金融市场中最实用的部分:
核心简化1:只用近似系数(低频趋势)
传统小波:分解 → 近似系数 + 细节系数(多层)
本次应用:只保留近似系数 → 直接得到平滑趋势
核心简化2:直接卷积,不做阈值去噪
传统小波:分解 → 阈值处理细节系数 → 重构
本次应用:直接卷积 → 得到平滑价格
核心简化3:忽略边界处理
传统小波:需要对信号边界进行对称延拓、周期延拓等处理
本次应用:只关注中间部分,边界误差可接受
实现方式:滤波器卷积
def convolve(src, coeffs, step):
"""
核心算法:用小波系数对价格序列做加权平均
src: 价格序列 [100000, 101000, 99000, ...]
coeffs: 小波系数 [0.483, 0.837, 0.224, -0.129]
step: 采样步长(用于多层级)
"""
sum_val = 0.0 # 加权和
sum_w = 0.0 # 权重和
for i, weight in enumerate(coeffs):
idx = i * step
if idx < len(src):
sum_val += src[idx] * weight
sum_w += weight
return sum_val / sum_w # 归一化
这个函数就是小波滤波器的核心:
step参数,实现多层级平滑(Level 1/2/3...)为什么这样简化是合理的?
因为交易的本质需求是:在噪音中找到趋势。小波变换的近似系数本身就是对信号的”低通滤波“,保留了低频趋势成分,这正是我们需要的。
完整的小波分析虽然更精确,但在金融交易中:
使用发明者量化(FMZ)平台的本地回测引擎,获取数据非常方便!
'''backtest
start: 2025-12-17 00:00:00
end: 2025-12-23 08:00:00
period: 1h
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT","fee":[0,0]}]
'''
from fmz import *
task = VCtx(__doc__)
def main():
exchange.SetCurrency("BTC_USDT")
exchange.SetContractType("swap")
records = exchange.GetRecords(PERIOD_H1, 500)
return records
records = main()
无需复杂的API对接和数据清洗,直接获取标准化的K线数据。这让我们能快速验证7种小波类型的实际效果,而不是陷入数据处理的泥潭。
通过对比7种常见小波类型(Haar、Daubechies 4、Symlet 4、Biorthogonal 3.3、Mexican Hat、Morlet、Discrete Meyer)在加密货币价格上的表现,直观展示:
重点不在于数学推导的严谨性,而在于实战效果的可视化对比,帮助交易者建立直观认识,选择适合自己策略的小波类型。
Haar小波是最基础的小波类型,系数只有两个:[0.5, 0.5],本质上就是对相邻两个价格做简单平均。
核心代码:
coeffs = [0.5, 0.5]
# 对价格序列 [100000, 101000, 99000, 102000, 98000] 处理
def smooth(prices, i):
return (prices[i] * 0.5 + prices[i-1] * 0.5) / 1.0
# 结果:[100000, 100500, 100000, 100500, 100000]
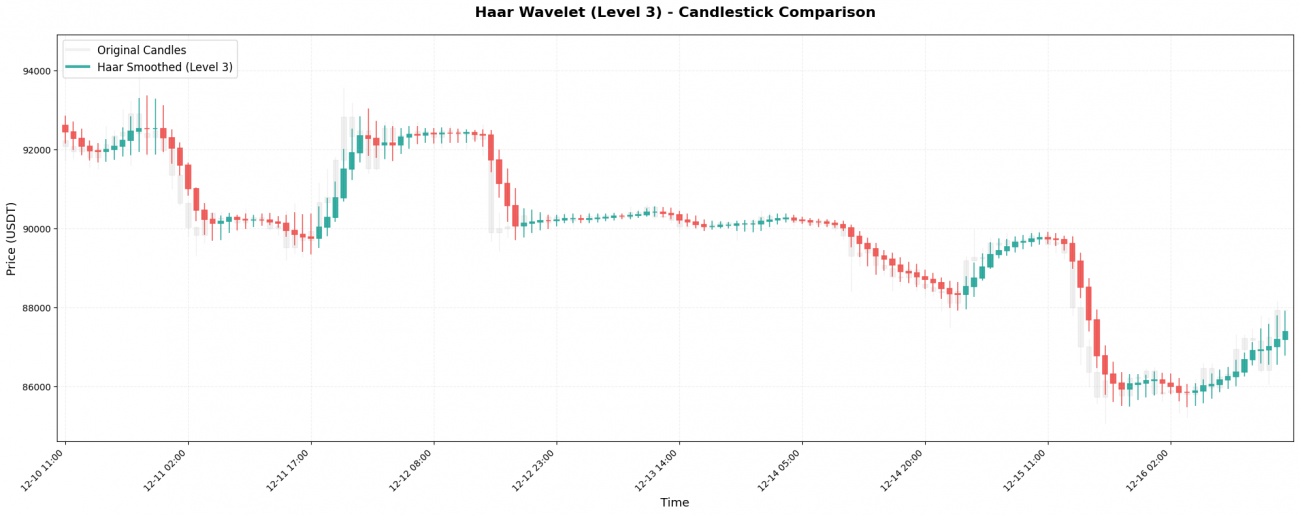
Daubechies 4(简称db4)是工程领域最常用的小波之一,系数:[0.483, 0.837, 0.224, -0.129]。注意最后一个系数是负数,这是它的独特之处。
核心代码:
coeffs = [0.483, 0.837, 0.224, -0.129]
# 处理第i个价格点
def smooth(prices, i):
weighted_sum = (prices[i] * 0.483 + # 当前价格
prices[i-1] * 0.837 + # 前1根,权重最大!
prices[i-2] * 0.224 + # 前2根
prices[i-3] * (-0.129)) # 前3根,负权重
weight_sum = 0.483 + 0.837 + 0.224 + (-0.129) # = 1.415
return weighted_sum / weight_sum
# 示例:smooth([100000, 101000, 99000, 102000], 3) ≈ 100251
关键特点: 前1根K线的权重(0.837)比当前价格(0.483)还大!这意味着db4更重视"刚刚发生的价格",负权重系数会对更早的价格产生"抵消"效果,进一步增强平滑性。
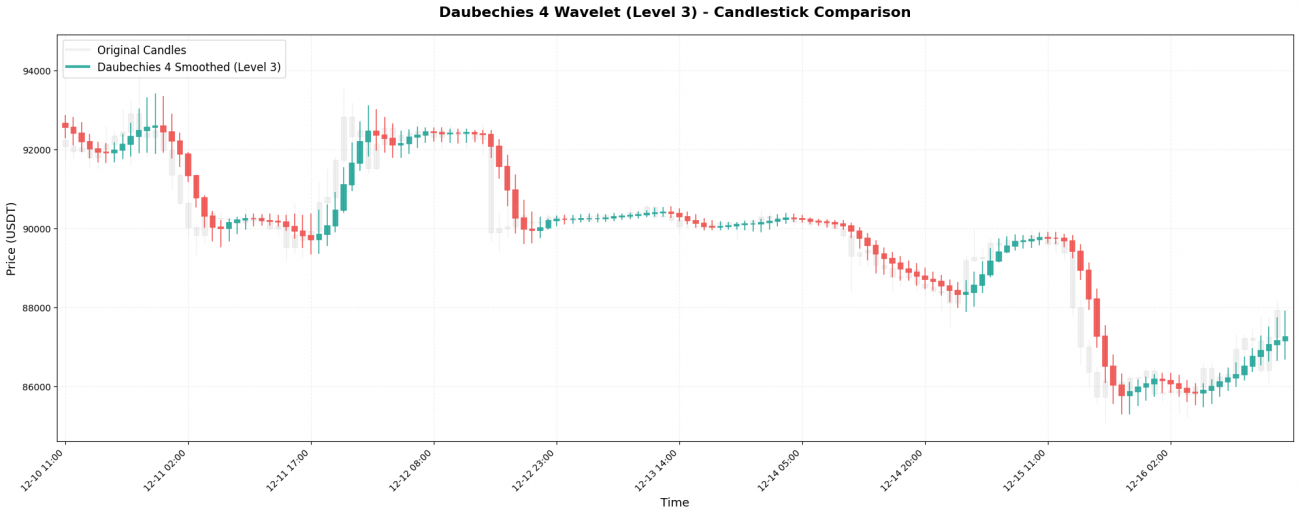
Symlet 4是Daubechies的改良版,追求更好的对称性。系数:[-0.076, -0.030, 0.498, 0.804, 0.298, -0.099, -0.013, 0.032]。
核心代码:
coeffs = [-0.076, -0.030, 0.498, 0.804, 0.298, -0.099, -0.013, 0.032]
# 向前看8根K线
def smooth(prices, i):
weighted_sum = sum(prices[i-j] * coeffs[j] for j in range(8))
weight_sum = sum(coeffs)
return weighted_sum / weight_sum
# 平滑效果比Haar和db4都强,但反应速度更慢
关键特点: 窗口长度8根K线,对价格的"记忆"更长。真正的趋势转折可能要8根K线之后才能在平滑曲线上看出来。
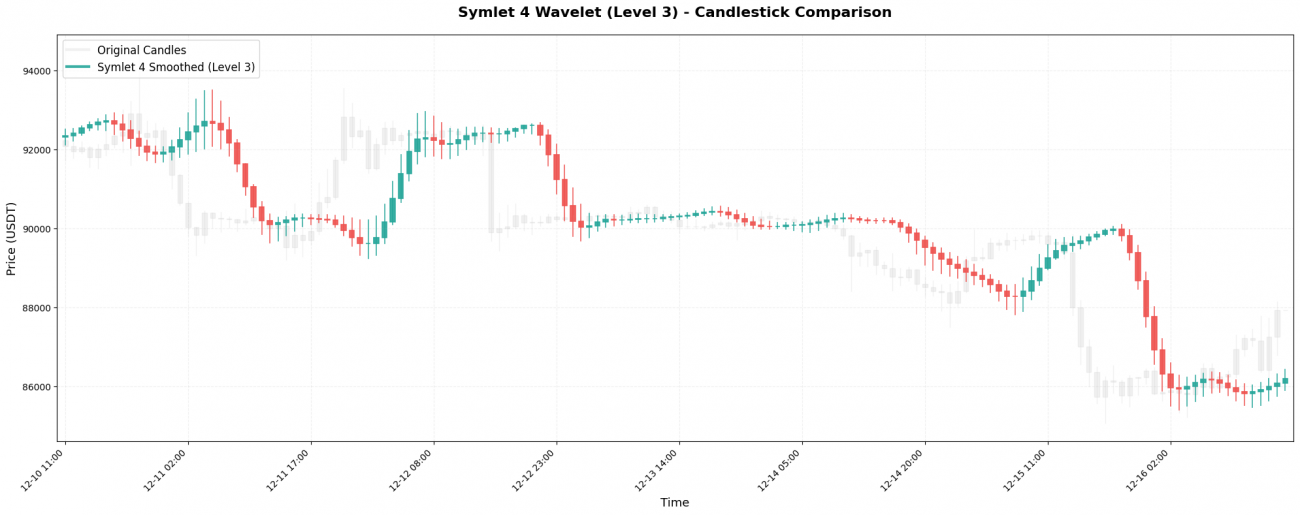
Biorthogonal 3.3(简称bior3.3)是完全对称的小波,系数:[-0.066, 0.283, 0.637, 0.283, -0.066]。
核心代码:
coeffs = [-0.066, 0.283, 0.637, 0.283, -0.066]
# ↑ 中心↑ ↑
# 完全对称的两端
# 处理中间价格点
def smooth(prices, i):
# 实际应用:只向前看,不使用未来数据
weighted_sum = (prices[i-4] * (-0.066) + # 前4根
prices[i-3] * 0.283 + # 前3根
prices[i-2] * 0.637 + # 前2根,权重最大
prices[i-1] * 0.283 + # 前1根
prices[i] * (-0.066)) # 当前
weight_sum = sum(coeffs) # = 1.071
return weighted_sum / weight_sum
关键特点: 对称性保证不会产生"相位失真" - 平滑后的曲线不会莫名其妙地向左或向右偏移。
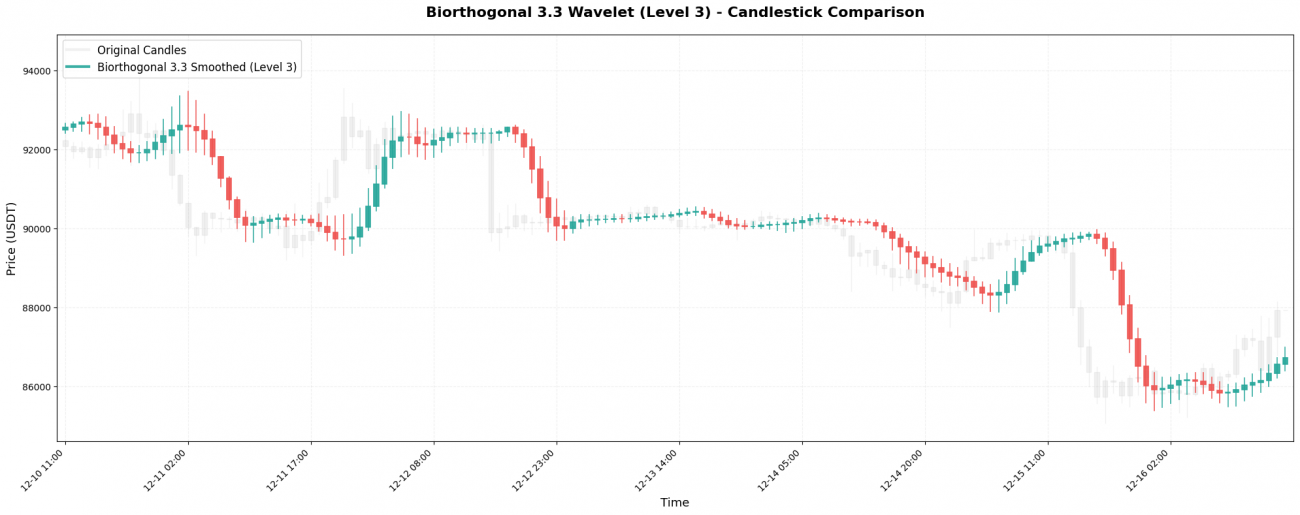
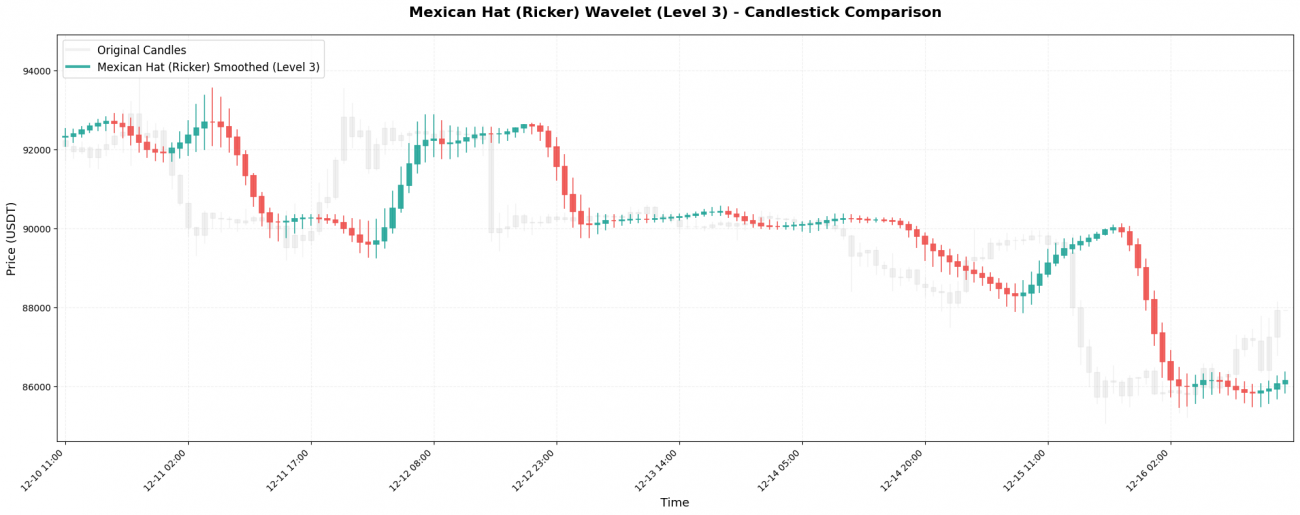
Mexican Hat(墨西哥帽,也叫Ricker小波)系数:[-0.1, 0.0, 0.4, 0.8, 0.4, 0.0, -0.1],形状像墨西哥草帽。
核心代码:
coeffs = [-0.1, 0.0, 0.4, 0.8, 0.4, 0.0, -0.1]
# 负值 零 正值 最大 正值 零 负值
# ↓ ↓
# "惩罚"两端,增强拐点检测能力
def smooth(prices, i):
weighted_sum = (prices[i-6] * (-0.1) + # 左3,负权重
prices[i-5] * 0.0 + # 左2
prices[i-4] * 0.4 + # 左1
prices[i-3] * 0.8 + # 中心,权重最大
prices[i-2] * 0.4 + # 右1
prices[i-1] * 0.0 + # 右2
prices[i] * (-0.1)) # 右3,负权重
weight_sum = sum(coeffs)
return weighted_sum / weight_sum
关键特点: "中间大,两端负"的结构让它特别擅长检测拐点 - 价格从上涨转为下跌(或反向)的关键时刻。负权重系数会对远端价格产生"惩罚",快速捕捉趋势变化。
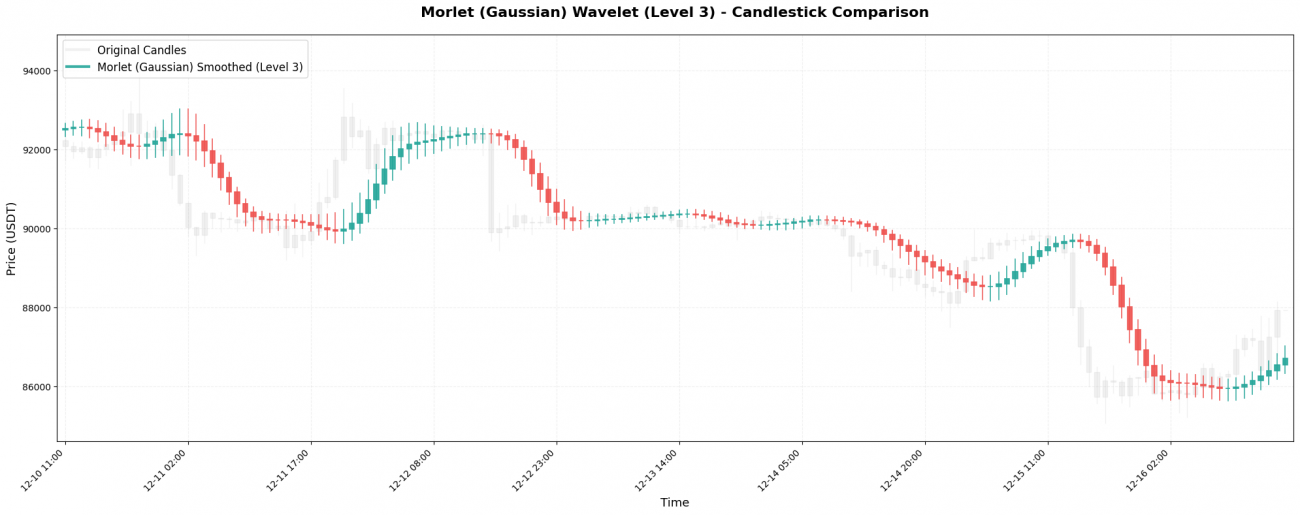
Morlet小波基于高斯分布(正态分布),系数:[0.0625, 0.25, 0.375, 0.25, 0.0625]。
核心代码:
coeffs = [0.0625, 0.25, 0.375, 0.25, 0.0625]
# ↓ ↓ ↓中心 ↓ ↓
# 远端 近端 最高 近端 远端
# 完美的高斯钟形曲线
def smooth(prices, i):
weighted_sum = (prices[i-4] * 0.0625 + # 左2,6.25%
prices[i-3] * 0.25 + # 左1,25%
prices[i-2] * 0.375 + # 中心,37.5%
prices[i-1] * 0.25 + # 右1,25%
prices[i] * 0.0625) # 右2,6.25%
# 权重和正好 = 1.0,无需除法
return weighted_sum
关键特点: 所有小波中最"温柔"的,无负权重,所有价格都被温柔纳入计算。产生的曲线极其平滑,但代价是反应慢 - 价格突变可能要好几根K线后才能体现。
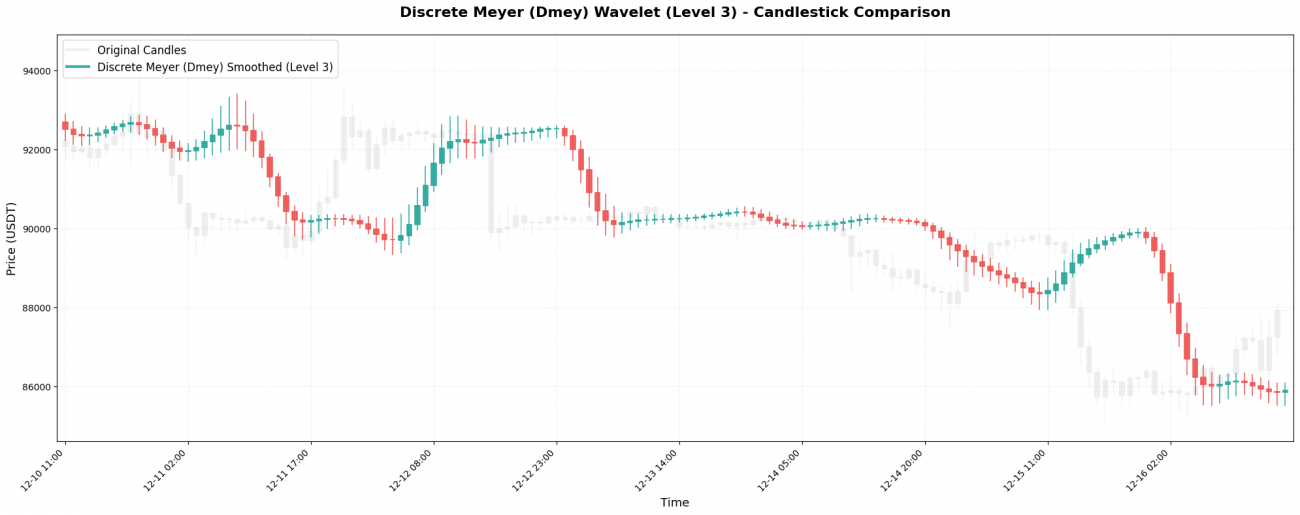
Discrete Meyer是最复杂的小波,系数:[-0.015, -0.025, 0.0, 0.28, 0.52, 0.28, 0.0, -0.025, -0.015]。
核心代码:
coeffs = [-0.015, -0.025, 0.0, 0.28, 0.52, 0.28, 0.0, -0.025, -0.015]
# ↑ ↑ ↑ ↑中心↑ ↑ ↑ ↑
# 完全对称,中心权重超过50%
def smooth(prices, i):
# 向前看9根K线
weighted_sum = sum(prices[i-j] * coeffs[j] for j in range(9))
weight_sum = sum(coeffs) # = 1.0
return weighted_sum
# 注意:第4根之前的K线权重是0.52,超过50%!
# 实际上在告诉你"4根K线之前的中期趋势"
关键特点: 系数最多(9个),看的历史最长,平滑效果最强。适合提取"周级别趋势",但延迟巨大 - 价格都跌10%了,它的曲线可能还显示"继续上涨"。
看完7种小波,你应该发现了规律:
系数越多 = 看的越远 = 平滑越强 = 延迟越大
Haar (2个系数) → 只看1根之前 → 几乎不平滑
Daubechies 4 (4个) → 看3根之前 → 轻度平滑
Mexican Hat (7个) → 看6根之前 → 中度平滑
Discrete Meyer (9个) → 看8根之前 → 重度平滑
负权重的作用 = 增强敏感度 = 更容易检测变化
Haar/Morlet (无负权重) → 温柔平滑,不敏感
Mexican Hat (两端负) → 对拐点敏感
Daubechies 4 (有负) → 对趋势变化敏感
对称性的作用 = 不失真 = 保持原有形态
非对称(Daubechies) → 可能向左/右偏移
对称(Biorthogonal/Meyer) → 保持中心位置
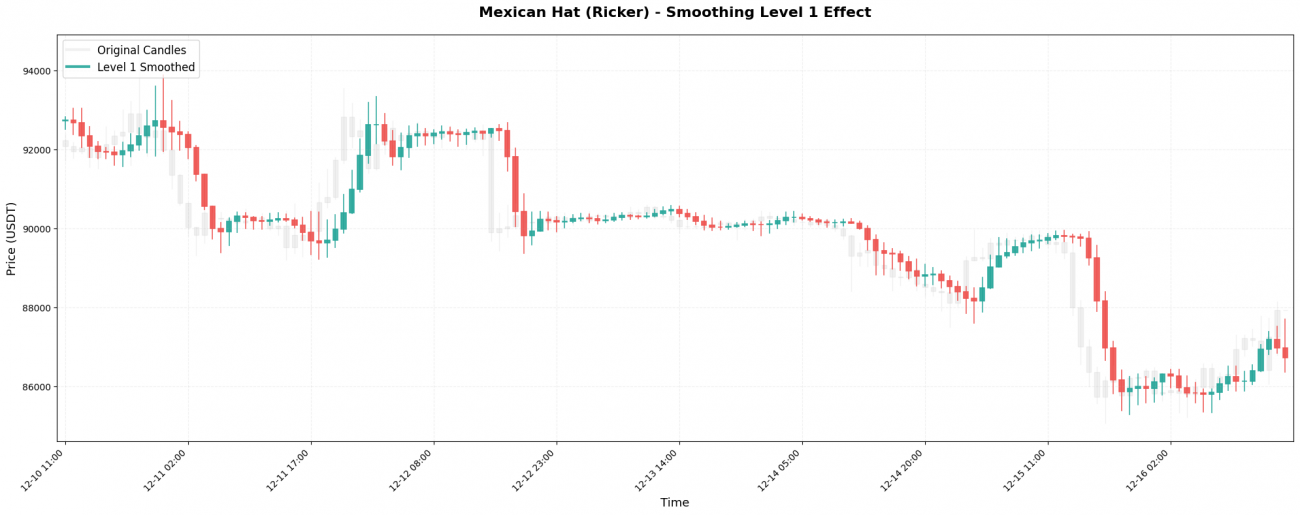
小波变换可以递归应用,就像套娃一样。第一次应用叫Level 1,对Level 1的结果再应用一次叫Level 2,以此类推。
不同层级看到的时间尺度:
假设用1小时K线做BTC交易:
Level 1 → 看2-4小时的短期波动
Level 2 → 看4-8小时的趋势
Level 3 → 看1-2天的中期趋势 (策略常用)
Level 4 → 看2-4天的波段
Level 5 → 看4-8天的大趋势
实际效果对比:
原始BTC价格(1小时线):99500, 99800, 99200, 100200, 99800, 100500, 100100, ...
Level 1处理: 99600, 99650, 99500, 99900, 99950, 100200, 100250, ...
(稍微平滑,还能看到波动)
Level 3处理: 99620, 99650, 99700, 99800, 99950, 100100, 100200, ...
(明显平滑,显示中期趋势)
Level 5处理: 99630, 99640, 99660, 99700, 99760, 99840, 99930, ...
(极度平滑,只显示大方向)
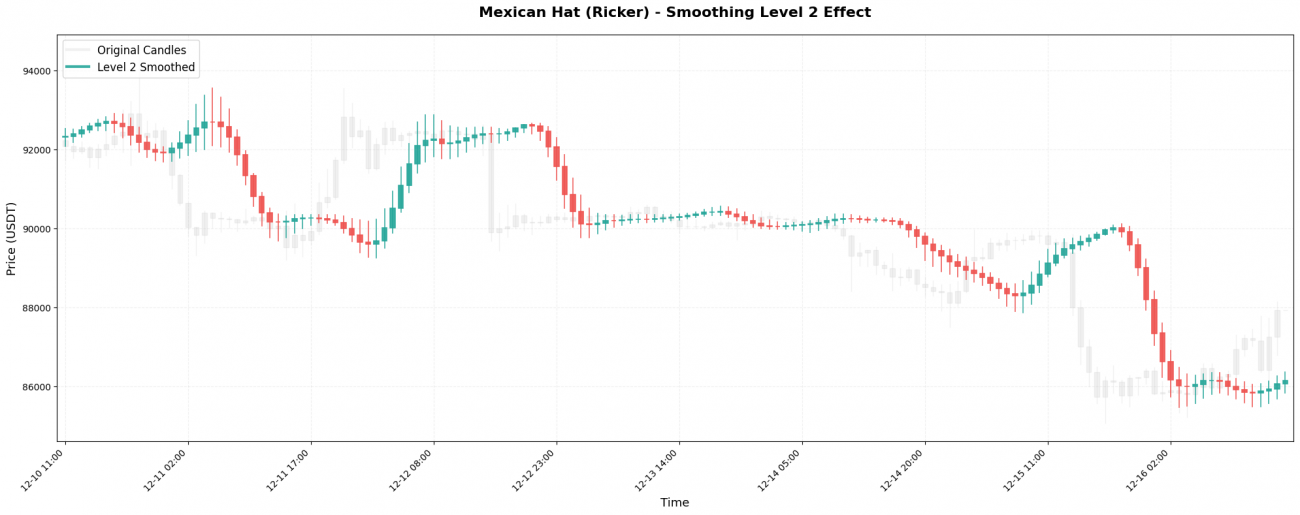
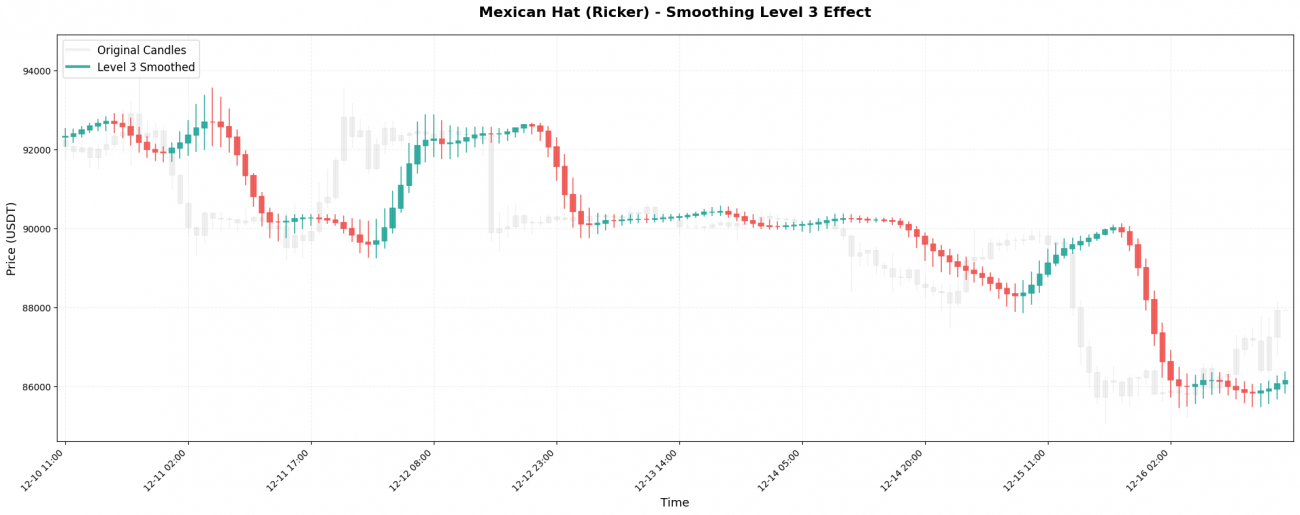
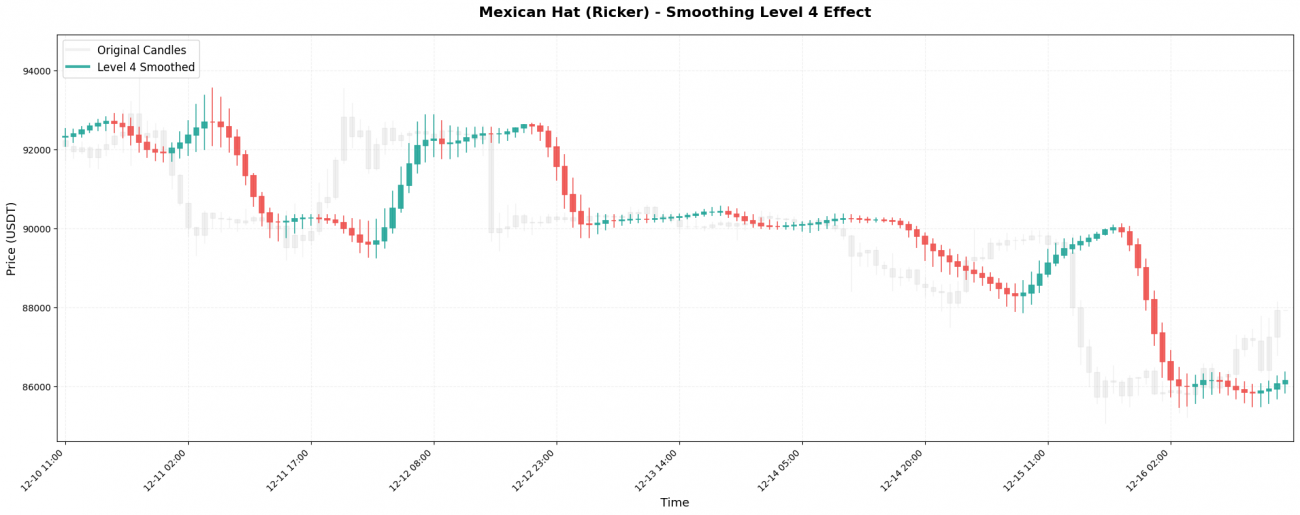
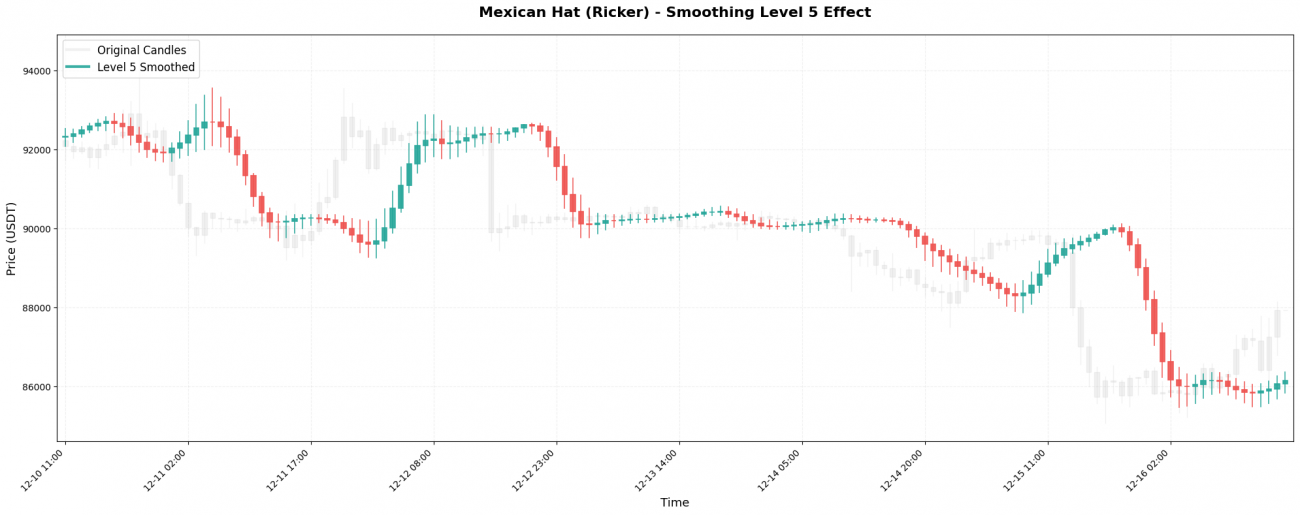
选择原则很简单:你的持仓周期有多长,就用对应的Level。
做15分钟超短线 → Level 1-2
做日内波段 → Level 2-3
做几天的swing → Level 3-4
做长线趋势 → Level 4-5
小波变换在交易中的应用非常直接:用它生成的平滑价格曲线来判断趋势方向,当趋势改变时就进行交易。具体来说,如果平滑后的收盘价比前一根高,说明趋势向上,就做多;如果平滑后的收盘价比前一根低,说明趋势向下,就平仓或做空。这个逻辑之所以有效,是因为小波已经把短期的随机波动过滤掉了,留下的"向上"或"向下"大概率是真实的趋势改变,而不是噪音造成的假信号。
# 执行小波变换
transformed = transformer.transform_ohlc(df)
# 获取最近两根K线的平滑收盘价
w_close_current = transformed['w_close'].values[-1] # 当前平滑收盘价
w_close_prev = transformed['w_close'].values[-2] # 前一根平滑收盘价
# 判断趋势方向
signal = 0
if w_close_current > w_close_prev:
signal = 1 # 平滑价格向上 → 做多
elif w_close_current < w_close_prev:
signal = -1 # 平滑价格向下 → 做空
# 获取账户信息
account = exchange.GetAccount()
ticker = exchange.GetTicker()
if not account or not ticker:
Log("[Warning] Failed to get account/ticker info")
Sleep(5000)
continue
current_price = ticker['Last']
Log(f"[Price] 原始: {df['Close'].values[-1]:.2f}, "
f"平滑当前: {w_close_current:.2f}, 平滑前值: {w_close_prev:.2f}")
Log(f"[Trend] {'↑ 向上' if signal == 1 else '↓ 向下' if signal == -1 else '→ 横盘'}")
# 执行交易逻辑
if signal == 1 and position != 1:
# 平滑价格向上 → 做多
Log(f"[信号] 趋势向上,开多 @ {current_price:.2f}")
if position == -1:
# 先平空仓
exchange.SetDirection("closesell")
exchange.Buy(current_price, 1)
Log(f"[平仓] 平空仓")
# 开多仓
exchange.SetDirection("buy")
exchange.Buy(current_price, 1)
Log(f"[开仓] 开多仓")
position = 1
elif signal == -1 and position != -1:
# 平滑价格向下 → 做空
Log(f"[信号] 趋势向下,开空 @ {current_price:.2f}")
if position == 1:
# 先平多仓
exchange.SetDirection("closebuy")
exchange.Sell(current_price, 1)
Log(f"[平仓] 平多仓")
# 开空仓
exchange.SetDirection("sell")
exchange.Sell(current_price, 1)
Log(f"[开仓] 开空仓")
position = -1
else:
Log(f"[持仓] 当前{'多头' if position == 1 else '空头' if position == -1 else '空仓'},无需操作")
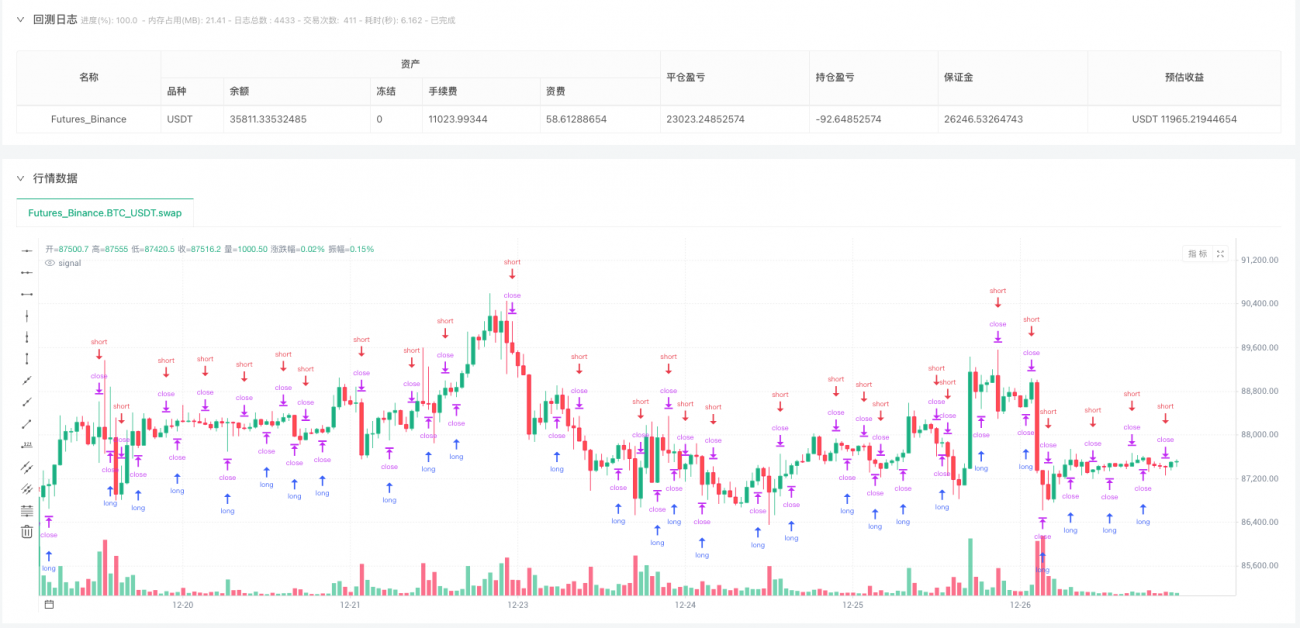
当然,实际使用中不会这么简单粗暴。你可以同时用多个Level的小波,比如Level 2显示短期趋势,Level 4显示长期趋势,只有当两者同向时才开仓,这样能大幅降低假信号。也可以加入其他过滤条件,比如要求成交量放大、波动率足够大、或者价格突破了某个关键位置,这些都能提高胜率。止损方面,可以用小波平滑价格的波动幅度来动态设置,比如跌破平滑价格减去2倍ATR就止损。仓位管理上,趋势越明显(平滑价格的斜率越大)就用越重的仓位,趋势不明朗就轻仓或观望。
但核心思路始终是一个:用小波把嘈杂的价格变成清晰的趋势,然后在清晰的趋势上做判断。这比直接在原始K线上看涨跌要靠谱得多,因为原始K线可能今天涨3%明天跌2%后天又涨4%,你根本分不清是趋势还是震荡,而小波处理后的曲线会告诉你"这段时间整体是向上的,虽然中间有波动"。
从实际平滑效果来看,小波变换在金融数据处理中的确能发挥一定作用:它可以过滤部分短期噪音,帮助提取相对清晰的趋势信息。但这项技术也存在明显局限性 ——滞后性问题无法完全避免,它只能处理历史数据,无法对未来走势做出预测。此外,单独使用小波变换的效果较为有限,需搭配其他分析方法与风控手段,才能构建起完整的交易系统。
这一局限的核心原因,在于金融市场的特殊性。在语音识别、图像处理等传统信号处理领域,噪音特征相对稳定,信号模式也会重复出现,因此小波变换能较好地实现信号与噪音的分离。但金融市场截然不同:今天被视为 “噪音” 的波动,明天可能成为反映市场变化的 “信号”;当下有效的分析模式,未来随时可能失效。市场本身是非平稳、动态变化的,不存在永恒不变的规律,这就要求小波变换在金融领域的应用必须结合具体市场环境灵活调整。
当你看到有人过度夸大小波变换、傅立叶变换的实际效果时,可以试着提出这些问题:选用的是哪种小波类型?选择该类型而非其他类型的依据是什么?平滑层级如何设定?是否有对应的回测结果与参数选择过程?真正具备专业知识的从业者,必然能清晰解释这些关键技术细节。
基于有限的知识储备,我们开展了此次实践探索,核心是用通俗的方式分享小波变换的应用思路,帮助大家对这项技术建立基本认知。对于深耕该领域的量化研究者,我们始终保持敬意;如果您是相关领域的专家,也欢迎指正文中不足 —— 比如小波参数选择的理论依据、多尺度组合的优化方法、自适应小波选择的实现路径等,我们将虚心吸纳建议,不断完善内容。