感知机是个相当简单的模型，但它既可以发展成支持向量机（通过简单地修改一下损失函数）、又可以发展成神经网络（通过简单地堆叠），所以它也拥有一定的地位。为方便，我们统一讨论二分类问题，并将两个类别的样本分别称为正、负样本。
感知机能做什么？
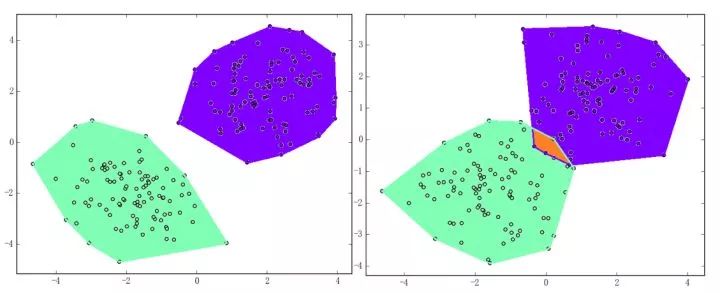
感知机能（且一定能）将线性可分的数据集分开。什么叫线性可分？在二维平面上、线性可分意味着能用一条线将正负样本分开，在三维空间中、线性可分意味着能用一个平面将正负样本分开。可以用两张图来直观感受一下线性可分（上图）和线性不可分（下图）的概念：
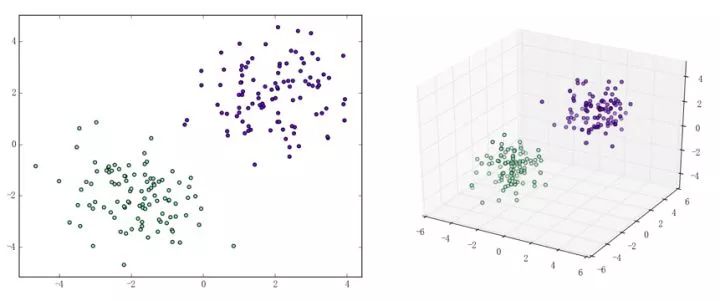
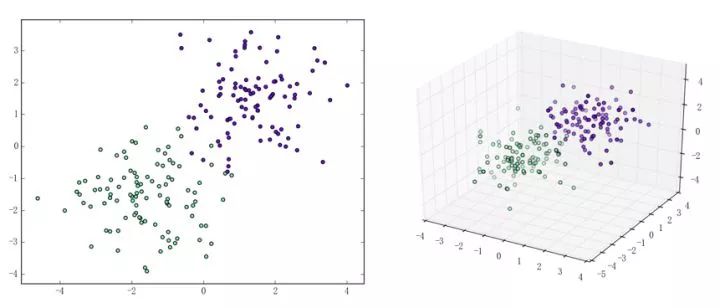
那么一个感知机将会如何分开线性可分的数据集呢？下面这两张动图或许能够给观众老爷们一些直观感受：
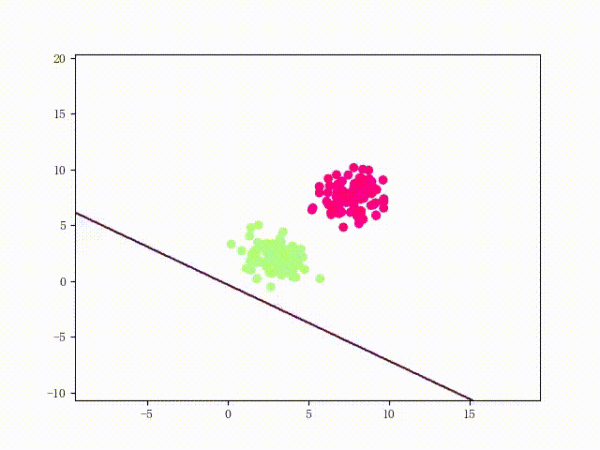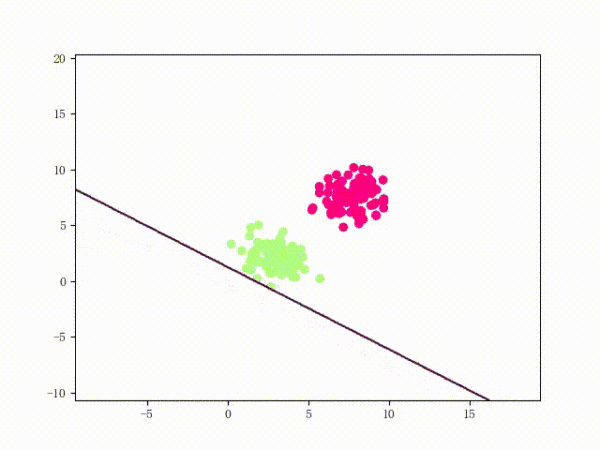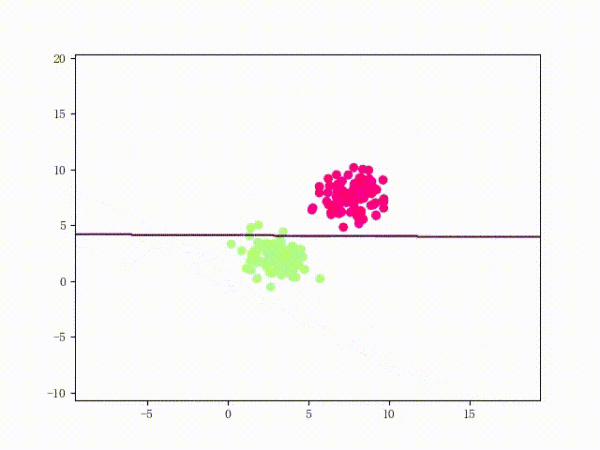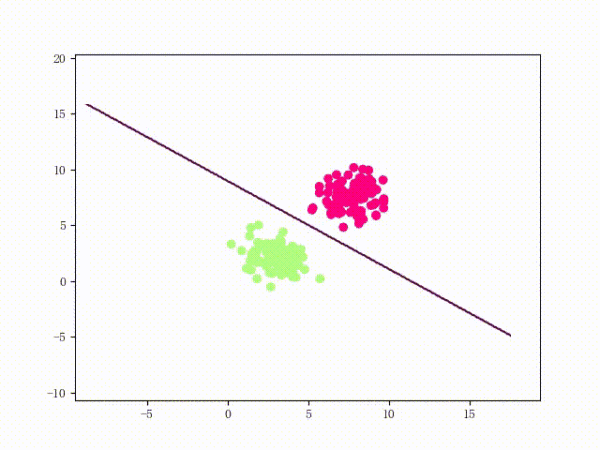
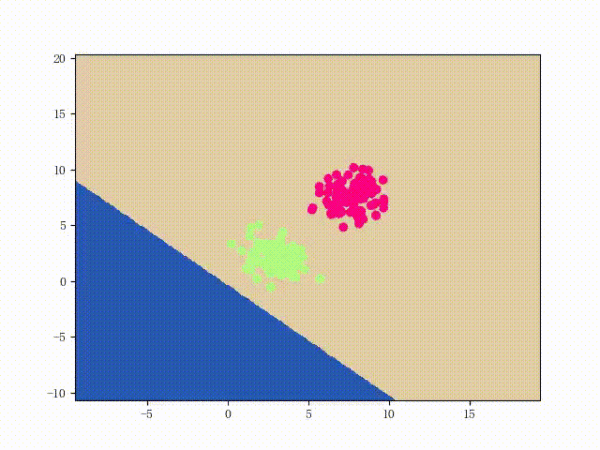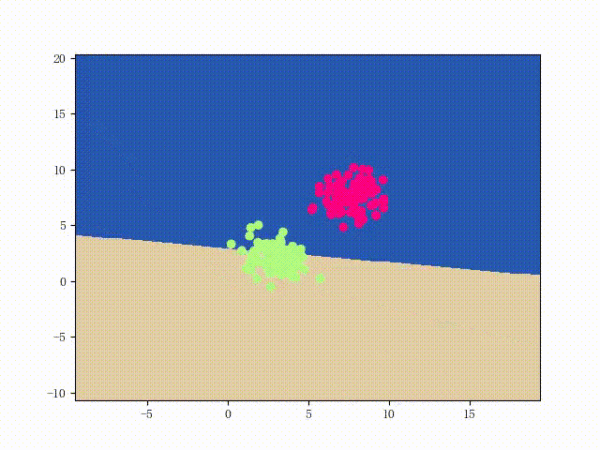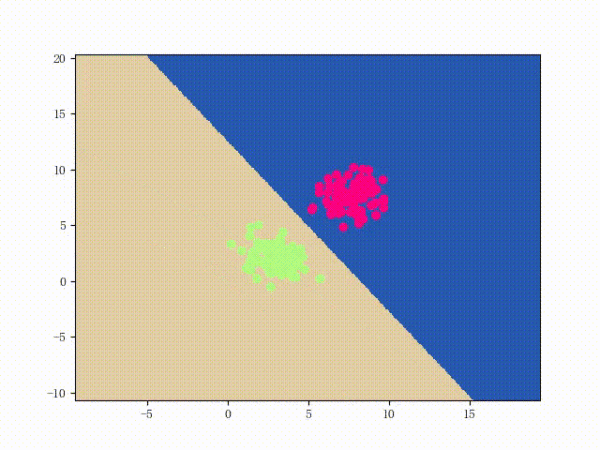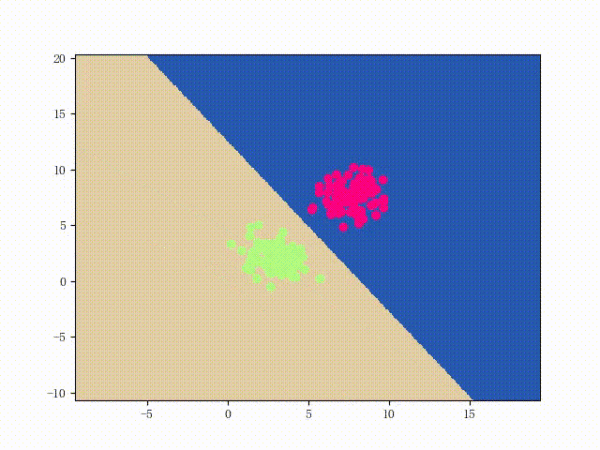
看上去挺捉急的，不过我们可以放心的是：只要数据集线性可分，那么感知机就一定能“荡”到一个能分开数据集的地方（文末会附上证明）
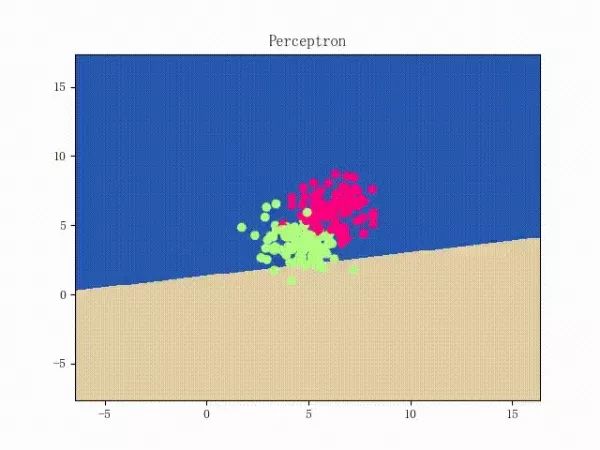
那么反过来，如果数据集线性不可分，那么感知机将如何表现？相信聪明的观众老爷们已经猜到了：它将会一直“荡来荡去”（最后停了是因为到了迭代上限）（然后貌似动图太大导致有残影……不过效果也不差所以就将就着看一下吧 ( σ'ω')σ）：
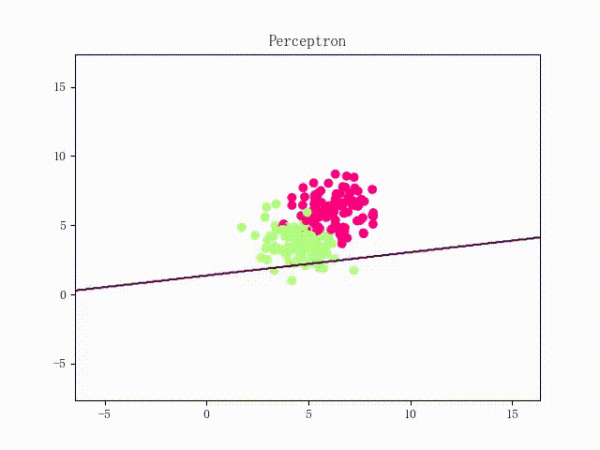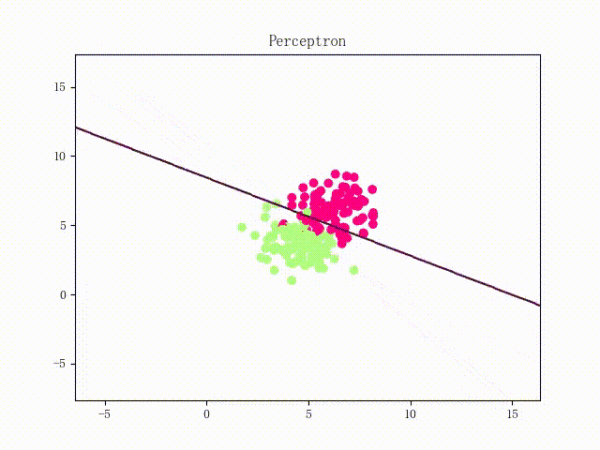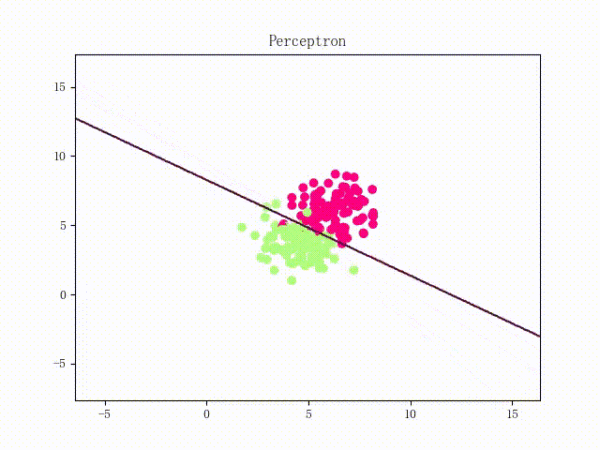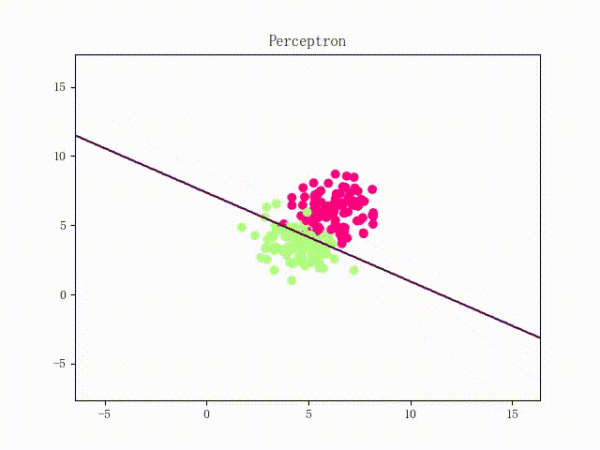
class Perceptron:
def __init__(self):
self._w = self._b = None
def fit(self, x, y, lr=0.01, epoch=1000):
# 将输入的 x、y 转为 numpy 数组
x, y = np.asarray(x, np.float32), np.asarray(y, np.float32)
self._w = np.zeros(x.shape[1])
self._b = 0.
上面这个 fit 函数中有个 lr 和 epoch，它们分别代表了梯度下降法中的学习速率和迭代上限（p.s. 由后文的推导我们可以证明，对感知机模型来说、其实学习速率不会影响收敛性【但可能会影响收敛速度】）
梯度下降法我们都比较熟悉了。简单来说，梯度下降法包含如下两步：
求损失函数的梯度（求导）
梯度是函数值增长最快的方向我们想要最小化损失函数我们想让函数值减少得最快将参数沿着梯度的反方向走一步
（这也是为何梯度下降法有时被称为最速下降法的原因。梯度下降法被普遍应用于神经网络、卷积神经网络等各种网络中，
那么对于感知机模型来说，损失函数是什么呢？注意到我们感知机对应的超平面为：
for _ in range(epoch):
# 计算 w·x+b
y_pred = x.dot(self._w) + self._b
# 选出使得损失函数最大的样本
idx = np.argmax(np.maximum(0, -y_pred * y))
# 若该样本被正确分类，则结束训练
if y[idx] * y_pred[idx] > 0:
break
# 否则，让参数沿着负梯度方向走一步
delta = lr * y[idx]
self._w += delta * x[idx]
self._b += delta
那么一个感知机将会如何分开线性可分的数据集呢？下面这两张动图或许能够给观众老爷们一些直观感受：
至此，感知机模型就大致介绍完了，剩下的则是一些纯数学的东西，大体上不看也是没问题的。
相关数学理论
亦即训练步数是有上界的，这意味着收敛性。而且中不含学习速率，这说明对感知机模型来说、学习速率不会影响收敛性。
最后简单介绍一个非常重要的概念：拉格朗日对偶性（Lagrange Duality）。我们在前三小节介绍的感知机算法，其实可以称为“感知机的原始算法”；而利用拉格朗日对偶性，我们可以得到感知机算法的对偶形式。鉴于拉格朗日对偶性的原始形式太过纯数学，所以我打算结合具体的算法来介绍、而不打算叙述其原始形式，在有约束的最优化问题中，为了便于求解、我们常常会利用它来将比较原始问题转化为更好解决的对偶问题。对于特定的问题，原始算法的对偶形式也常常会有一些共性存在。比如对于感知机和后文会介绍的支持向量机来说，它们的对偶算法都会将模型的参数表示为样本点的某种线性组合、并把问题转化为求解线性组合中的各个系数。
虽说感知机算法的原始形式已经非常简单，但是通过将它转化为对偶形式、我们可以比较清晰地感受到转化的过程，这有助于理解和记忆后文介绍的、较为复杂的支持向量机的对偶形式。
考虑到原始算法的核心步骤为：
此即感知机模型的对偶形式。需要指出的是，在对偶形式中、样本点里面的x仅以内积的形式（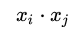
）出现；这是一个非常重要且深刻的性质，利用它和后文将进行介绍核技巧、能够将许多算法从线性算法“升级”成为非线性算法。
注意到对偶形式的训练过程常常会重复用到大量的、样本点之间的内积，我们通常会提前将样本点两两之间的内积计算出来并存储在一个矩阵中；这个矩阵就是著名的 Gram 矩阵、其数学定义即为：
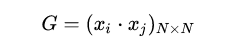
从而在训练过程中如果要用到相应的内积、只需从 Gram 矩阵中提取即可，这样在大多数情况下都能大大提高效率。
