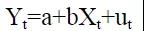协整检验
协整是分析这样的问题的:在什么情况下,两个或两个以上的醉汉合在一起走路,旁边观察的人会发现这样的特征,如果把这几个醉汉看做一个整体的话,会发现他们走路的特征不是醉汉,而是正常人。那么,在什么样的条件下,会出现上述现象呢?第一,这两个醉汉之间拴了一根绳子,类比数学上的线性组合;第二,这两个醉汉在走路时的用力方向,恰恰相反且相互抵消,即白噪声过程。
那么,从数学上来说,协整分析的本质就是,当两个或几个非平稳的时间序列数据的变化趋势相互抵消时,那么,它们的线性组合所得到的组合变量,就是平稳的。所以,如果我们发现两个经济变量之间是存在协整关系的,那么这表明,从长期来看,它们之间是存在一个均衡关系的。
下面以两变量的Engle-Granger检验阐述检验过程:
- 第一步:对两变量进行单位根平稳性检验,要求非平稳且同阶单整;
- 第二步:用OLS方法估计方程
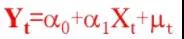 ,其为协整回归,之后计算非均衡误差,即
,其为协整回归,之后计算非均衡误差,即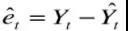 ;
;
- 第三步:检验非均衡误差的平稳性,检验方法依然是ADF检验。
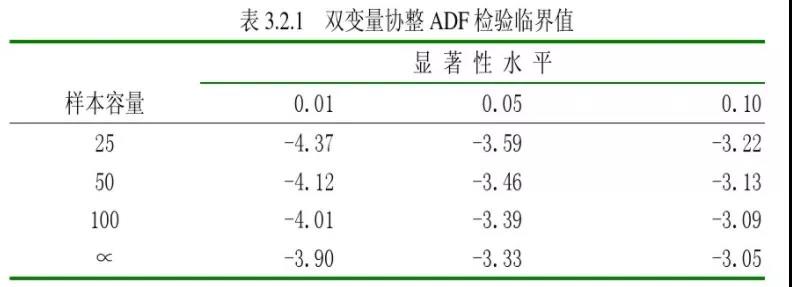
下面给出残差项ADF检验的临界值表:
假定有如下的一个单方程模型: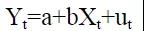
协整的含义就是同阶单整的两个或多个变量(比如,都是I(k)单整)之间的线性组合可能是I(k-1)的,故如果两个变量都是I(1)的,那么如果它们是协整的,则它们的线性组合是I(0)的,即是平稳的。故单方程协整检验的思想实际就是最后检验随机扰动项即残差项的平稳性,因为残差项本身就是两变量Y与X的一个线性组合,因此,如果残差项是平稳的,那么表明Y与X之间存在协整关系。
说说我对统计套利的几点想法吧
- 1、统计套利的核心在于找到接近白噪声的平稳过程;
- 2、平稳过程的统计性质不随时间t而变化,均值、方差为常数,自协方差与时间点t无关,只与时间跨度有关,当然,自相关系数呈指数级递减的越快越好即拖尾性没那么严重,偏自相关系数越早截尾越好。
- 3、对同一阶单整I(1)的变量X与Y做协整回归后,若得到的残差项为I(0)即协整,该检验方法等价于X与Y的一阶差分序列做平稳性检验后得到I(0)的结果,这不就是我们做统计套利所希望得到的结果吗。
相关推荐:
套利专题之四——误差修正模型
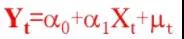 ,其为协整回归,之后计算非均衡误差,即
,其为协整回归,之后计算非均衡误差,即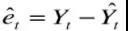 ;
;